This is the third post about project which creates new Smart Contract programming language with go. In the previous post, we’ve introduced you the motivation of this project, why we decided to built new Smart Contract language and brief architecture, and how we implement the first component lexer.

The project still WIP and open source so you can visit github.com/DE-labtory/koa and feel free to contribute to our project.

Part 1 — Motivation to make new Smart Contract programming language
Part 2 — How can we make our own Lexer?— Using State and Action

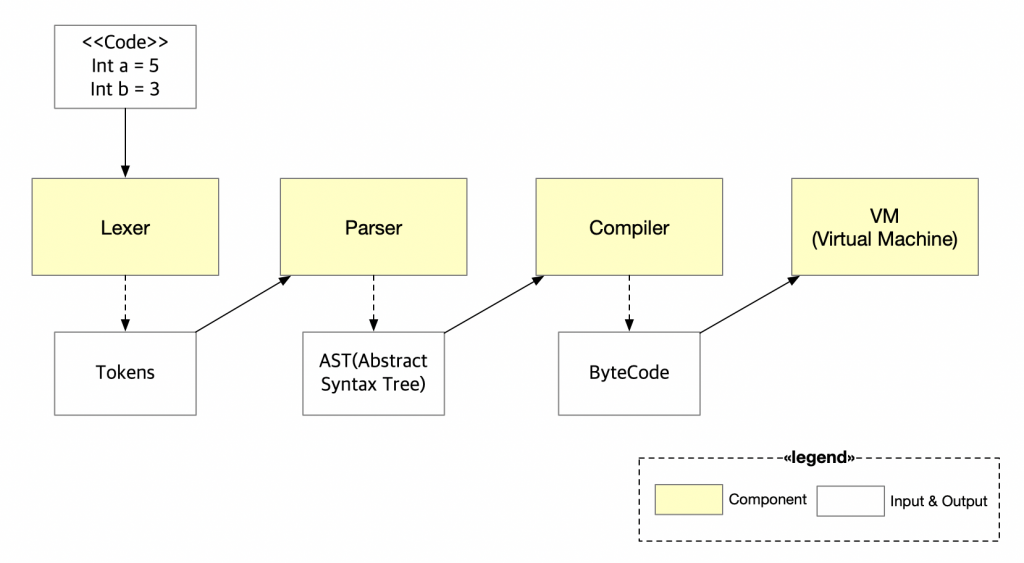
Our project consists of four components: Lexer, Parser, Compiler, VM. And in this post we’re going to talking about what is Parser, how can we make our own Parser with go.

What is Parser?

Everyone who has ever programming before maybe heard about parser, if not you can guess parser do parsing at least 🙂 Yes everyone know that. Then what is parsing exactly? Wikipedia explains what is parsing quite intuitively.

A parser is a software component that takes input data (frequently text) and builds a data structure — often some kind of parse tree, abstract syntax tree or other hierarchical structure — giving a structural representation of the input, checking for correct syntax in the process.

Parsing is process which builds data structure with its input data.

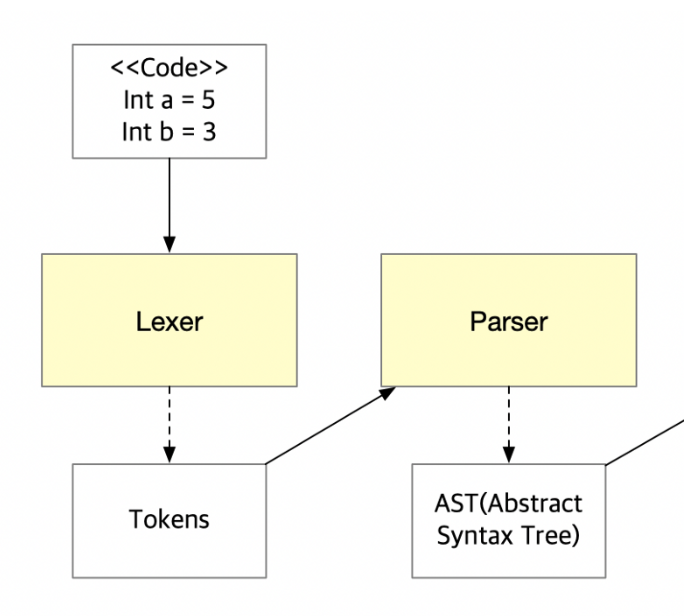
This is cropped version of our architecture which emphasize Parser’s input and output. As you can see the diagram, parser fed tokens from lexer, than creates data structure called Abstract Syntax Tree(AST). Also while parser builds data structure, checks whether given inputs are valid for representing data structure: Is inputs are in right order?, Is one of inputs illegal?

Yes I know, too abstract. Let’s take the example.

> var input = '{"msg": "hello, world"}';
> var output = JSON.parse(input);
> output
> { msg: 'hello, world' }
> output.msg
'hello, world'

I brought simple javascript code. You can test them on your own browser console. Inputs are given as string which has values as '{"msg": "hello, world"}' and assigned to input variable. Then you pass those input to the parser which is behind the JSON.parse function. The result is output , the data structure which stores the data with key, value, we called it as ‘object’ in javascript. But how we call it is not important, what we have to pay attention to is parser converted plain string to something which can store the data, object, data structure.

How about we pass this string to the parser? What would happen?

> var input = '{"msg": "hello, world"';

The result is

> var output = JSON.parse(input);
Uncaught SyntaxError: Unexpected end of JSON input
> output
undefined

Error. Input string '{"msg": "hello, world"' is not enough to make object. Parser check that while making object with those characters. And as I mentioned this is the second role of the parser; checking the given inputs whether it is valid to make data structure.

Until now we have been looking at how JSON parser works. But… what about our parser? This should be different with JSON parser? The answer is yes and no. On conceptual level, there’s no difference between JSON parser and ours. Both make data structure with given inputs and while making these data structure, validates input.

But the difference is JSON parser takes string as input, ours takes tokenized source code generated by lexer and JSON parser generate object but ours generate Abstract Syntax Tree(AST).

What is AST?

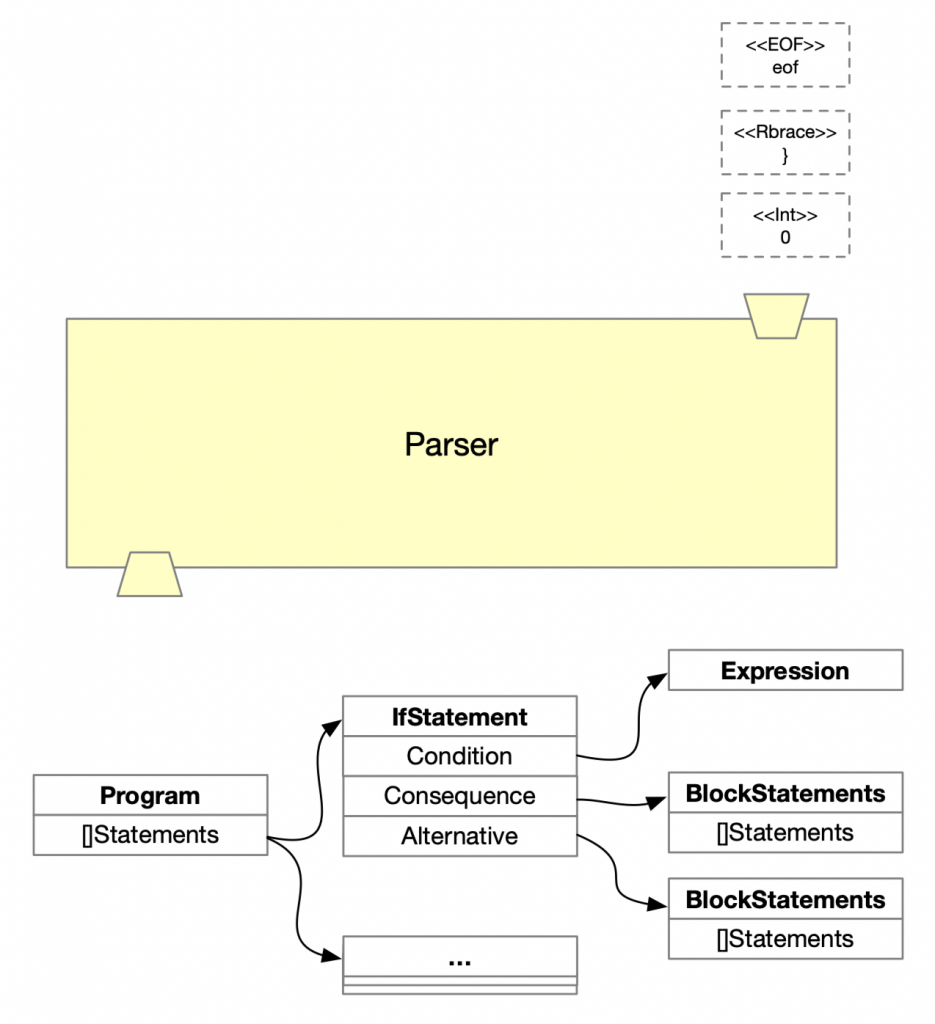
parser AST logical view — AST logical diagram

Most of interpreter and compiler use AST to represent source code. But as you know, AST is data structure so there’s not one true, the concept is the same, but they differ in details for each programming language. I think that diagram is not enough so I brought real one.

# source code
let a = 1;# AST
{
  "type": "Program",
  "body": [
    {
      "type": "VariableDeclaration",
      "declarations": [
        {
          "type": "VariableDeclarator",
          "id": {
            "type": "Identifier",
            "name": "a"
          },
          "init": {
            "type": "Literal",
            "value": 1,
            "raw": "1"
          }
        }
      ],
      "kind": "let"
    }
  ],
  "sourceType": "module"
}

Once again, javascript. There’s lots of online AST generator, so you can make it and test it on your own.

As you can see some informations are omitted such as semicolon, assign operator. That’s why we call it “abstract” syntax tree, we only left what we need.

Design and Implementation

We’ve seen what is parser, what is AST, the basic concept of the parser. Now let’s get into detail and think of it with code.

Create AST

First, we should create AST, that is what parser generate. AST is tree so let’s create node which consists of our ASTree.

// Node represent ast node
type Node interface {
   String() string
}

And there are two types of node: statement, expression

Statement vs Expression

What are these? What is difference between two? Before explaining about what is this, these are statements and expressions in our programming language.

Statement

int a = 1
return foo
if (a == 1) {} else {}
func foo() {}

Expression

add(1, 2)
1 * (2 +3)
a++

You may get the hint what is it and what is difference. Statement do not produce a value itself but do something whereas Expression produce value itself. But what exactly an expression is or a statement, depends on the programming language. For example, there could be such an expression

int b = if (a == 1) { return a } // assign 'a' to 'b', if 'a' is 1

In this case if-else could be an expression.

And these are our statement node and expression node.

// Represent Statement
type Statement interface {
   Node
   do()
}
// Represent Expression
type Expression interface {
   Node
   produce()
}

Contract

We’ve done to create our nodes of tree. Before we move on to next level, I’ll show you how our Smart Contract looks like.

contract {
    func sendMoneyTo(id string) {
        // logic here
    }
    func receiveMoney(id string) {
        // logic here
    }
    ...
}

As you can see, our contract starts with contract keyword and inside the block, there are set of functions client can use.

I show you how our Smart Contract looks like first because I hope this can help you to understand our root node of AST; Contract.

// Represent Contract.
// Contract consists of multiple functions.
type Contract struct {
   Functions []*FunctionLiteral
}
func (c *Contract) do() {}
func (c *Contract) String() string { /* return strings */ }

Quite intuitive, isn’t it? Contract implements Statement and Contract has Functions which represents functions in contract like sendMoneyTo and receiveMoney. And this is our FunctionLiteral

// FunctionLiteral represents function definition
// e.g. func foo(int a) string { ... }
type FunctionLiteral struct {
   Name       *Identifier
   Parameters []*ParameterLiteral
   Body       *BlockStatement
   ReturnType DataStructure
}
func (fl *FunctionLiteral) do() {}
func (fl *FunctionLiteral) String() string { /* return strings */ }

Name represent function name, Parameters for function parameters, Body for function body which contains function logic, ReturnType for return type fo function, quite straightforward.

Until now we’ve seen big picture of how AST could be implemented. I decided not to describe all the details how each AST node could be implemented, because it is quite redundant and boring. If you want to see how other nodes are implemented, you can see the source code here

Create Parser

We’ve seen how our AST could be implemented. And it’s time to implement our parser. I know you did not forgot but I will summarize what parser do again:

take input data(tokens) and builds a data structure(AST).
check the given inputs whether it is valid to make data structure.

When designing a parser I thought one thing:

It would be better if parser don’t keep the pointer of tokens

Because I thought it is not the responsibility of parser, just reading the token from something and parsing it is the only thing parser should do.

TokenBuffer

So created ‘TokenBuffer’ concept. TokenBuffer keeps tokens pointer and client can read or peek the token from it. With TokenBuffer we can make our parser much compact, we see this later.

// TokenBuffer provide tokenized token, we can read from this buffer
// or just peek the token
type TokenBuffer interface {   
   // Read retrieve token from buffer. and change the
   // buffer states
   Read() Token
   // Peek take token as many as n from buffer but not change the
   // buffer states
   Peek(n peekNumber) Token
}

And this is our TokenBuffer interface. It has two methods Read() and Peek(n peekNumber) , our parser will use it to retrieve tokens to parsing.

Parser? No, Parsing Functions

After we create TokenBuffer and decided to pass this TokenBuffer to parsing functions as parameter, we could say “There’s no need to create parser structure and its method!”. And someone could say “What is advantage of making it as function not method?”.

Well, I think one of advantage of making it as function is we could test each parsing function easily. If we make parsing function as method, every time we test the methods we should make parser structure first, and check whether parser states is not impact on its method logic. Yes, function is stateless only parameters can change its behavior, same inputs same results.


func Parse(buf TokenBuffer) (*ast.Contract, error) {   
   contract := &ast.Contract{}
   contract.Functions = []*ast.FunctionLiteral{}
   ...
   for buf.Peek(CURRENT).Type == Function {
      fn, err := parseFunctionLiteral(buf)
      if err != nil {
         return nil, err
      }
      contract.Functions = append(contract.Functions, fn)
   }
   ...
   return contract, nil
}

This is the entry point to parsing function. Parse takes TokenBuffer as we talk before and in the for loop parsing Smart Contract’s functions.

Also similar to AST part, I decided not to describing all the details how each parsing function implemented all has similar idea, and quite easy to understand, if you want to see how each statements can be parsed, you can see the source code from here. Instead I’m going to focus on the complex problem, parsing expression.

How to parse expression?

One of the big problems when implementing parser is to decide how to parse expression. Let’s take a look at why it is difficult.

1 +2
1 +2 + 3
1 / 2 +3 % 4
1 / (2 + 3) % 4
1 / ((2 + 3) % 4) + 5
1 / ((2 + 3) % 4) + 5 + add(1, 2) 1 / ((2 + 3 + add(1, 2)) % 4) + 5
…

We can feel that parsing all of these expression correctly in a consistent way is not a simple problem even by a glance. So before we move on, take a breathe and let’s see why it is difficult.

1 + 2 * 3 ===> (1 + (2 * 3))
1 * 2 + 3 ===> ((1 * 2) + 3)

First, each token has its own precedence. For example, parser should know that ‘asterisk’ token has higher precedence than ‘plus’ token when grouping expression, similarly

1 * 2 + 3   ===> ((1 * 2) + 3)
1 * (2 + 3) ===> (1 * (2 + 3))

‘parentheses’ have higher precedence than ‘asterisk’.

- 1 - 2

Second, each token can have different meaning depending on its position. For example, first ‘minus’ and next ‘minus’ should be handled differently, first could be handled as prefix ‘minus’ and second as infix ‘minus’.

Pratt Parser comes to rescue!

And we can solve this problem in a Pratt Parser way. It was first described by Vaughan Pratt in the 1973 paper “Top down operator precedence”.

Then what is Pratt Parser? why we decided to use it? One of the key features of this parsing is for each token we define several parsing functions. (there’s one more, I will show you in a few seconds)

Advantage of this parsing is easy to make, easy to understand, easy to scale which quite fits to our needs.

In our parser using Pratt Parsing way, we should define at most two parsing function for each token type. One is prefix parsing function for parsing token as prefix expression, the other is infix parsing function for parsing token as infix expression.

type (
    prefixParseFn func(TokenBuffer) (ast.Expression, error)
    infixParseFn  func(TokenBuffer, ast.Expression) (ast.Expression, error)
)
var prefixParseFnMap = map[TokenType]prefixParseFn{}
var infixParseFnMap = map[TokenType]infixParseFn{}

These are declaration of type of prefix/infix parsing function and maps which store parsing functions for each token type.

func initParseFnMap() {
    prefixParseFnMap[Int] = parseIntegerLiteral
    prefixParseFnMap[Minus] = parsePrefixExpression
    ...   
    infixParseFnMap[Minus] = parseInfixExpression
    ...
}

In the case of ‘minus’, ‘minus’ can be used as infix or prefix (we saw it as example above) so define parsePrefixExpression in the prefixParseFnMap and parseInfixExpresion in the infixParseFnMap

And as I mentioned before, each token type has its own precedence which tell us which token type should be grouped first. In the code above, we can see that Asterisk has higher precedence than the Plus and Lparen has higher precedence than Asterisk.

Next section is about parseExpression function and I think that this is the hardest part to understand in this post because of the second feature of Pratt Parser: recursive descent

parseExpression function

func parseExpression(buf TokenBuffer, pre precedence) (ast.Expression, error) {
    exp, err := makePrefixExpression(buf)
    ...   
    exp, err = makeInfixExpression(buf, exp, pre)
    ...
    return exp, nil
}

parseExpression function abstracted with two function: makePrefixExpression , makeInfixExpression. With abstraction we can easily grasp whole flow of parseExpression, start from first token which is first token of whole expression, parse it as prefix expression if possible, then parse it as infix expression with the left tokens.

// makePrefixExpression retrieves prefix parse function from
// map, then parse expression with that function if exist.
func makePrefixExpression(buf TokenBuffer) (ast.Expression, error) {
   curTok := buf.Peek(CURRENT)
   fn := prefixParseFnMap[curTok.Type]
   ...   exp, err := fn(buf)
   ...
   return exp, nil
}

In makePrefixExpression, check whether current token has prefix parsing function, if so, parsing current token with fn prefix parsing function, after that return results.

// MakeInfixExpression retrieves infix parse function from map
// then parse expression with that function if exist.
func makeInfixExpression(buf TokenBuffer, exp ast.Expression, pre precedence) (ast.Expression, error) {   
    expression := exp   
    for !curTokenIs(buf, Semicolon) && pre < curPrecedence(buf) {
        token := buf.Peek(CURRENT)
        fn := infixParseFnMap[token.Type]
        ...
        expression, err = fn(buf, expression)
        ...
   }   
   return expression, nil
}

And… this is makeInfixExpression Ok… I said this section is hardest and the reason for that is because of this function makeInfixExpression. And I think this is the right time to take the example, greatest tool to understand something we first met.

parseExpression function example

What we are going to parse is this.

- 1 + 2 * 3 == after parsing ==> ((-1) + (2 * 3))

And you may remember that parser fed tokens from TokenBuffer. So we can imagine that parser will receive tokens like this.

----------------------TokenBuffer-------------------------
    parser   <- |  -  |  1  |  +  |  2  |  *  |  3  |  ;  |
----------------------------------------------------------

Then… Let’s start parsing expression!

----------------------TokenBuffer-------------------------
    parser   <- |  -  |  1  |  +  |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func parseExpression(buf TokenBuffer, pre precedence) (ast.Expression, error) {
   // pre: LOWEST   
   exp, err := makePrefixExpression(buf) <-- done prefix parsing#1
   exp, err = makeInfixExpression(buf, exp, pre)
   return exp, nil
}

Enter into makePrefixExpression, later done prefix parsing#1 will be used as mark.

----------------------TokenBuffer-------------------------
    parser   <- |  -  |  1  |  +  |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func makePrefixExpression(buf TokenBuffer) (ast.Expression, error) {
   curTok := buf.Peek(CURRENT) <-- [ - ]   
   fn := prefixParseFnMap[curTok.Type] <-- fn: parsePrefixExpression
   exp, err := fn(buf)
   return exp, nil
}

Peeked token is ‘minus’ and its prefix parse function is parsePrefixExpression I’ll not show you the whole function, but what we need.

----------------------TokenBuffer-------------------------
    parser   <- |  1  |  +  |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func parsePrefixExpression(buf TokenBuffer) (ast.Expression, error) {
    tok := buf.Read()  <-- [ - ]
    op := operatorMap[tok.Type]
    right, err := parseExpression(buf, PREFIX) <-- recursive#1
    ...
}

We can see that Pratt Parser recursive descent. Call parseExpression again.

----------------------TokenBuffer-------------------------
    parser   <- |  1  |  +  |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func makePrefixExpression(buf TokenBuffer) (ast.Expression, error) {
    curTok := buf.Peek(CURRENT) <-- [ 1 ]   
    fn := prefixParseFnMap[curTok.Type] <-- fn: parseIntegerLiteral
    exp, err := fn(buf)
    return exp, nil
}

Peeked token is ‘integer’ and its prefix parse function is parseIntegerExpression

----------------------TokenBuffer-------------------------
    parser   <- |  +  |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func parseIntegerLiteral(buf TokenBuffer) (ast.Expression, error) {
    token := buf.Read() <-- [ 1 ]
    value, err := strconv.ParseInt(token.Val, 0, 64)
    lit := &ast.IntegerLiteral{Value: value}
    return lit, nil
}

Then we return twice, then our pc is now on the recursive#1 point, and return once again. And now we built (-1) expression! and we are on the done prefix parsing#1, move on to makeInfixExpression.

----------------------TokenBuffer-------------------------
    parser   <- |  +  |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func makeInfixExpression(buf TokenBuffer, exp ast.Expression, pre precedence) (ast.Expression, error) {
    expression := exp
    for !curTokenIs(buf, Semicolon) && pre < curPrecedence(buf) {
        token := buf.Peek(CURRENT) <-- [ + ] 
        fn := infixParseFnMap[token.Type] <-- parseInfixExpression#1
        expression, err = fn(buf, expression)
    }   
    return expression, nil
}

As ‘plus’ is not semicolon and has higher precedence than LOWEST, so enter the loop, also ‘plus’ has parseInfixExpression infix parsing function.

----------------------TokenBuffer-------------------------
    parser   <- |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func parseInfixExpression(buf TokenBuffer, left ast.Expression) (ast.Expression, error) {
    curTok := buf.Read() <-- [ + ]
    expression := &ast.InfixExpression{
        Left:     left, <-- [ (-1) ]
        Operator: operatorMap[curTok.Type], <-- [ + ]
    }
    precedence := precedenceMap[curTok.Type] <-- [ SUM ]
    expression.Right, err = parseExpression(buf, precedence) <-- recursive#2
    return expression, nil
}

Recursive again, but at this time execute parseExpression with precedence SUM

----------------------TokenBuffer-------------------------
    parser   <- |  2  |  *  |  3  |  ;  |
----------------------------------------------------------
func makePrefixExpression(buf TokenBuffer) (ast.Expression, error) {
    curTok := buf.Peek(CURRENT) <-- [ 2 ]   
    fn := prefixParseFnMap[curTok.Type] <-- fn: parseIntegerLiteral
    exp, err := fn(buf) <-- IntegerLiteral{2}
    return exp, nil
}
----------------------TokenBuffer-------------------------
    parser   <- |  *  |  3  |  ;  |
----------------------------------------------------------
func parseIntegerLiteral(buf TokenBuffer) (ast.Expression, error) {
    token := buf.Read() <-- [ 2 ]
    value, err := strconv.ParseInt(token.Val, 0, 64)
    lit := &ast.IntegerLiteral{Value: value}
    return lit, nil
}

At this point we’ve created IntegerLiteral{Value:2} and assigned it to exp, then enter to makeInfixExpression with precedence SUM!

----------------------TokenBuffer-------------------------
    parser   <- |  *  |  3  |  ;  |
----------------------------------------------------------
func makeInfixExpression(buf TokenBuffer, exp ast.Expression, pre precedence) (ast.Expression, error) {
    expression := exp <-- IntegerLiteral
    for !curTokenIs(buf, Semicolon) && pre < curPrecedence(buf) {
        /* we get into the loop! */      
        token := buf.Peek(CURRENT) <-- [ * ] 
        fn := infixParseFnMap[token.Type] <-- parseInfixExpression#2
        expression, err = fn(buf, expression)
    }
    return expression, nil
}

Here is the KEY PART! Because we compare ‘plus’ precedence which is SUM with ‘asterisk’ precedence which is PRODUCT, we get into the loop!

----------------------TokenBuffer-------------------------
    parser   <- |  3  |  ;  |
----------------------------------------------------------
func parseInfixExpression(buf TokenBuffer, left ast.Expression) (ast.Expression, error) {
    curTok := buf.Read() <-- [ * ]
    expression := &ast.InfixExpression{
        Left:     left, <-- [ 2 ]
        Operator: operatorMap[curTok.Type], <-- [ * ]
    }
    precedence := precedenceMap[curTok.Type] <-- [ PRODUCT ]
    expression.Right, err = parseExpression(buf, precedence) <-- recursive#3
    return expression, nil
}

I would skip a little bit, in recursive#3, create IntegerLiteral{Value: 3} and this is assigned to expression.Right. Now we’ve done to group (2 * 3), before we group 1 + 2! This is because PRODUCT have higher precedence than SUM so that we can get into for-loop and grouped.

----------------------TokenBuffer-------------------------
    parser   <- |  ;  |
----------------------------------------------------------
func makeInfixExpression(buf TokenBuffer, exp ast.Expression, pre precedence) (ast.Expression, error) {
    expression := exp <-- IntegerLiteral
    for !curTokenIs(buf, Semicolon) && pre < curPrecedence(buf) { <-- because of semicolon, we can't get into this loop      
        token := buf.Peek(CURRENT) <-- was [ * ]
        fn := infixParseFnMap[token.Type] <-- parseInfixExpression#2
        expression, err = fn(buf, expression)
    }   
    return expression, nil
}

After make (2 * 3) expression, we return to parseInfixExpession#2, and we left semicolon in the TokenBuffer, so that we return from makeInfixExpression

----------------------TokenBuffer-------------------------
    parser   <- |  ;  |
----------------------------------------------------------
func makeInfixExpression(buf TokenBuffer, exp ast.Expression, pre precedence) (ast.Expression, error) {
    expression := exp
    for !curTokenIs(buf, Semicolon) && pre < curPrecedence(buf) {
        token := buf.Peek(CURRENT) <-- was [ + ] 
        fn := infixParseFnMap[token.Type] <-- parseInfixExpression#1
        expression, err = fn(buf, expression)
    }   
    return expression, nil
}

Then at the recursive#2 we can see that (2 * 3) expression becomes right expression of (-1) +, then return to parseInfixExpression#1. Finally we made ((-1) + (2 * 3))

Through this example we can feel that Pratt Parser is recursive — recursively call parseExpression and make leaf node. And every time we get into for loop in makeInfixExpression our AST is getting deeper.

Conclusion

Whew… And… Thats it! We’ve gone through from the very basic concept of the parser — what is parser?, what is AST? And how we can implement our own parser from design to code base implementation. Also we discuss about how we can parse lots of complex expression in a consistent way, the solution was Pratt Parsing. It has two key features, one is defining parsing function for each token type, the other was it is quite recursive descent. In the next post we’ll cover about compiler part.

Create New SmartContract Programming Language with Go — Parser Part